5. 자료구조 (Heap, Hash)
- 힙 (Heap)
- 해시 (Hash)
- 해시 충돌 (Hash Collision)
1. 힙 (Heap)
1.1. 힙이란?
비선형 자료구조로서, 여러 개의 값들 중에서 최대값이나 최소값을 빠르게 찾아내도록 만들어졌다. 힙은 일종의 반 정렬 상태(느슨한 정렬 상태) 를 유지한다. 또한 BST 와는 다르게 중복된 값을 허용한다.
이를 활용하여 우선순위 큐 를 구성할 수 있다!!
1.2. 힙의 종류
최대 힙(max heap)
부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
최소 힙(min heap)
부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리

1.3. 힙의 구현
힙을 저장하는 표준적인 자료구조는
배열이다특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다
힙에서 부모 노드와 자식노드의 관계
- 왼쪽 자식 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식 인덱스 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스) / 2
#include <iostream>
#include <cstring>
#define MAX_N 20
using namespace std;
class Heap {
private:
int heap[MAX_N + 1];
int heap_size;
public:
// 생성자
Heap(){
memset(heap, 0, sizeof(heap));
heap_size = 0;
}
// Print
void printHeap(){
for(int i=1; i<=heap_size; i++){
cout << heap[i] << " ";
}
cout << "\n";
}
// Heapify
void heapify(int h,int m){
int item = heap[h];
int i;
for(i=h*2; i<=m; i*=2){
// 자식 노드 중, 더 큰 노드를 찾음
if(i<m && heap[i]<heap[i+1]) i++;
// 타겟노드가 자식노드보다 크다면 중단
if(item >= heap[i]) break;
// 그렇지 않다면 타겟노드 위치에 자식노드 삽입
else heap[i/2] = heap[i];
}
heap[i/2] = item;
}
// Insert
void insert_max_heap(int item){
int i = ++heap_size;
// Root 노드가 아니고, item 이 부모보다 크다면
while(i != 1 && item > heap[i/2]){
heap[i] = heap[i/2];
i /= 2;
}
heap[i] = item;
}
// Delete
int delete_max_heap(){
int root = heap[1];
// 마지막 노드를 루트 노드로 설정
heap[1] = heap[heap_size--];
// 줄어든 크기를 다시 heapify
heapify(1, heap_size);
return root;
}
// Swap
void swap(int a,int b){
int tmp = heap[a];
heap[a] = heap[b];
heap[b] = tmp;
}
// Sort
void heapsort(){
for(int i=heap_size/2; i>=1; i--){
heapify(i, heap_size);
}
for(int i=heap_size; i>=1; i--){
swap(1,i);
heapify(1, i-1);
}
}
};
2. 해시 (Hash)
2.1. 해시 함수 (Hash Function)
데이터의 효율적인 관리를 목적으로 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수이다. 이 때, 매핑 전 원래의 데이터 값을 키(key) , 매핑 후 데이터의 값을 해시값(hash value) , 매핑하는 과정 자체를 해싱(hashing) 이라고 한다.
나눗셈 법 (Division Method)
H(k) = k mod m
- 키(key)를 m값으로 나눈 나머지를 해시값으로 사용한다
- m은 2의 제곱수와 거리가 먼 소수를 선택하는 것이 좋음
- 다시 말해, 해시함수 특성 때문에 해시테이블 크기가 정해진다는 단점을 갖고 있음
곱셈 법 (Multiplication Method)
- 소수가 아닌 m을 택해야 하는 경우 사용
- m의 값이 중요하지 않음
- 계산을 간단하게 하기 위해, 보통 2의 거듭제곱을 사용
유니버셜 해싱 (Universal Hasing)
- 다수의 해시함수를 만들고, 이 해시함수의 집합 H에서 무작위로 해시함수를 선택해 해시값을 만드는 기법
- H에서 무작위로 뽑은 해시함수가 주어졌을 때, 임의의 키값을 임의의 해시값에 매핑할 확률을
1/n로 만드는 것이 목적 (n : 해시 테이블 크기)
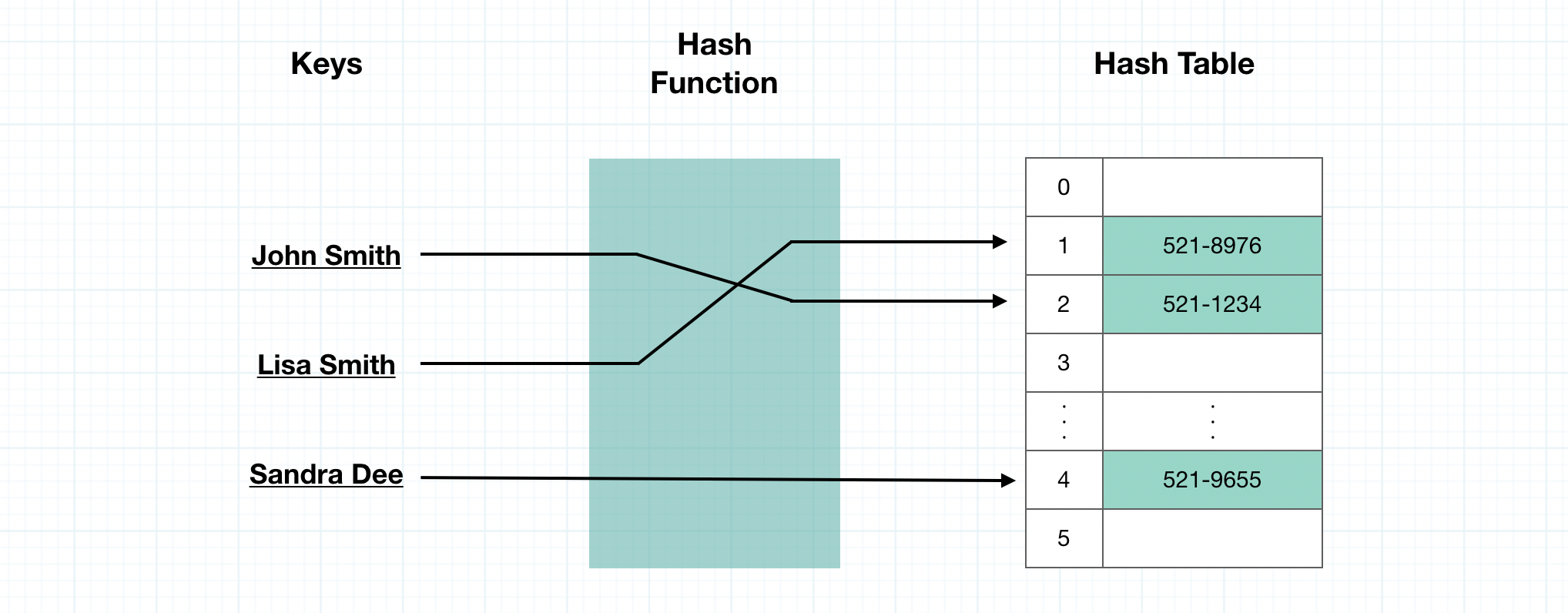
2.2. 해시 테이블 (Hash Table)
해시함수를 사용하여 키를 해시값으로 매핑하고, 이 값을 색인(index) 혹은 주소 삼아 데이터 값을 키와 함께 저장하는 자료구조를 해시 테이블 이라고 한다. 해시 테이블의 기본 연산은 삽입, 삭제, 탐색 이다.
3. 해시 충돌 (Hash Collision)
해시 함수는 해시값의 개수보다 대개 많은 키값을 해시값으로 변환하기 때문에, 해시함수가 서로 다른 두 개의 키에 대해 동일한 해시값을 내는 해시 충돌(hash collision) 이 발생하게 된다.
3.1. 연쇄법 (Chaining)
충돌이 발생했을 경우 각 데이터를 해당 주소에 있는 Linked List 에 삽입하여 문제를 해결하는 방법이자 개방 해싱 알고리즘이다.
삽입, 삭제, 탐색의 연산
- 새 데이터를 Linked List 의
head에 삽입한다 (데이터 삽입 시,O(1)의 시간이 걸림)- 탐색의 경우는 Linked List 를
순차 탐색해야한다는 단점을 가짐- 삭제 또한, 탐색과 마찬가지로 순차 탐색을 통해 값을 찾아야함

3.2. 개방 주소법 (Open Addressing)
충돌이 일어나면 해시 테이블 내의 새로운 주소를 탐사하여 충돌된 데이터를 입력하는 방식이다.
선형 탐사 (Linear Probing)
해시 충돌이 발견되면, 현재 주소에서 고정 폭으로 다음 주소로 이동하는 방법
- 점유된 위치가 연속적으로 나타나며 뭉치가 점점 커지는
클러스터(Cluster)현상이 자주 발생
제곱 탐사 (Quadratic Probing)
해시 충돌이 발견되면, 고정폭으로 이동하는 선형 탐사와는 달리 이동폭이 제곱수로 늘어나는 방법
- 서로 다른 해시값을 갖는 데이터에 대해서는 클러스터를 방지할 수 있지만, 같은 해시값을 갖는 데이터에 대해서는
2차 클러스터발생
이중 해싱 (Double Hashing)
탐사할 해시값의 규칙성을 없애버려 클러스팅을 방지하는 기법이다. 2개의 해시함수를 준비해 하나는 최초의 해시값을 얻을 때, 또 다른 하나는 해시충돌이 일어났을 때 탐사 이동폭을 얻기 위해 사용한다. 이렇게 되면 최초 해시값이 같도라도 탐사 이동폭이 달라지고, 탐사 이동폭이 같더라도 최초 해시값이 달라져 1~2차 클러스터를 모두 완화할 수 있다.
- 평균적으로 선형 탐사보다 적은 탐사 횟수를 가짐
- 선형 탐사에 비해 작은 테이블 크기를 가지고도 동일한 탐색 성능을 나타냄
재해싱 (Rehashing)
해시 테이블의 크기를 늘리고, 늘어난 해시 테이블의 크기에 맞춰 테이블 내의 모든 데이터를 다시 해싱하는 방법
3.3. 해시와 이진 트리
이진 트리보다 해시를 많이 사용하는 이유
- 간단하고 빠른 탐색 시간
이진 트리의 장점
- 동적 (삽입 횟수를 미리 알고있지 않아도됨)
- 최악의 경우 성능을 보장 (해싱의 경우 아무리 좋은 해시 함수라도 모든 값을 같은 장소로 해싱하는 경우가 발생할 수 있음)
- 사용할 수 있는 연산의 종류가 많음 (ex. Sorting)
# 간단한 해시 구현
#include <iostream>
using namespace std;
int hashTable[10000];
int _strlen(char *input){
int i = 0;
while(input[i] != '\0'){
i++;
}
return i;
}
int split(char *str){
int ret = 0;
int len = _strlen(str);
for(int i=0; i<len; i++){
ret += str[i] - '0';
}
return ret;
}
int main(int argc, const char * argv[]) {
// cin,cout 속도향상
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
while(1){
char key[10];
int value;
cout << "key >> ";
cin >> key;
cout << "value >> ";
cin >> value;
int hashKey = split(key);
if(!hashTable[hashKey]){
hashTable[hashKey] = value;
cout << "[SUCCESS] Key and value have been saved.\n";
}else{
cout << "[FAIL] The key already exists.\n";
break;
}
cout << "\n";
}
return 0;
}
# 연결리스트를 사용한 해시 구현
#include <iostream>
using namespace std;
const int PN = 23;
const int HASH_SIZE = 5;
char data[100][100];
int data_index = 1;
int hash_table[HASH_SIZE][10];
/*
데이터를 해시값으로 변환하는 함수
overflow?
: 오버플로우가 발생해도 같은 해시값을 도출하면 되므로 상관이 없음
unsigned?
: 해시값을 배열의 인덱스로 사용하기 위해 음수 X
*/
unsigned int get_key(char _data[]){
unsigned int key = 0, p = 1;
for(int i=0; _data[i] != 0; i++){
key += (_data[i] * p);
p *= PN;
}
return (key % HASH_SIZE);
}
/*
두 문자열을 비교하는 함수
*/
int my_strcmp(char a[],char b[]){
int i = 0;
while(a[i]) {
if(a[i] != b[i]) break;
i++;
}
return (a[i] - b[i]);
}
/*
해시에 데이터가 있는지 검사하는 함수
있다면 index 를 리턴
*/
int contain(char _data[]){
unsigned int key = get_key(_data);
int h_size = hash_table[key][0];
for(int i=1; i<=h_size; ++i){
int n_pos = hash_table[key][i];
if(my_strcmp(data[n_pos], _data) == 0){
return n_pos;
}
}
return -1;
}
/*
입력 받은 String 값을 추가하는 함수
1. name 배열에 string 값 복사
2. string 값을 해시 값으로 변환
3. 해시테이블에 인덱스 값을 넣어줌
*/
void add(char _data[]){
int len;
for(len=0; _data[len] != 0; len++){
data[data_index][len] = _data[len];
}
data[data_index][len] = 0;
unsigned int key = get_key(_data);
int& h_size = hash_table[key][0];
hash_table[key][++h_size] = data_index;
data_index++;
}
/*
입력 받은 String 값을 해시테이블에서 제거하는 함수
1. string 값을 해시값으로 변환
2. 해당값이 존재하는지 체크
3. 존재한다면 제거 후, 오른쪽값을 왼쪽으로 한 칸씩 땡기고 true 리턴
4. 존재하지 않는다면, false 리턴
*/
bool remove(char _data[]){
unsigned int key = get_key(_data);
int& h_size = hash_table[key][0];
for(int i=1; i<=h_size; i++){
int n_pos = hash_table[key][i];
if(my_strcmp(data[n_pos], _data) == 0){
int j;
for(j=i+1; j<=h_size; j++){
hash_table[key][j-1] = hash_table[key][j];
}
h_size--;
hash_table[key][j-1] = 0;
return true;
}
}
return false;
}
int main(int argc, const char * argv[]) {
// cin,cout 속도향상
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
for(int i=0; i<5; i++){
char input[100];
cin >> input;
add(input);
}
char input[100];
cin >> input;
remove(input);
return 0;
}
참고 자료
'CS > Algorithm' 카테고리의 다른 글
| [AL] 7. 최소 비용 신장 트리(MST) 알고리즘 (0) | 2019.04.17 |
|---|---|
| [AL] 6. Union-Find 알고리즘 (0) | 2019.04.05 |
| [AL] 4. 자료구조 (Graph) (0) | 2019.04.01 |
| [AL] 3. 자료구조 (Linked List, Stack, Queue) (0) | 2019.03.28 |
| [AL] 2. 자료구조 (Tree) (0) | 2019.03.11 |
